Por Lautaro Pérez Alcaraz

En un mundo cada vez más incierto y volátil debido a las múltiples variables que pueden afectar la valuación de un activo, el riesgo se ha convertido en una constante dentro del ámbito financiero y del mercado de capitales.

La volatilidad es una de las variables utilizadas y representa la incertidumbre sobre el precio futuro de un activo. Es decir, es la medida del nivel de fluctuaciones del precio de un determinado activo.

La volatilidad implícita nos aproxima a la volatilidad esperada de un activo financiero en el futuro. A diferencia de la volatilidad histórica, que se basa en los datos de precios del pasado, la volatilidad implícita se deriva del precio actual del mercado de opciones de ese activo. La interpretación más común es que representa una previsión sobre las verdaderas fluctuaciones de los mercados.

La misma no es calculada estadísticamente, al contrario, esta es hallada a partir de los precios de las opciones que se negocian en los diferentes mercados. Esta volatilidad se calcula a partir de opciones Call y Put ATM (At The Money) que coticen en el mercado ya que en estos casos el precio de ejercicio de la opción es igual o muy cercano al precio actual del activo subyacente.

¿Qué es una opción financiera?

Una opción financiera es un contrato que otorga a su comprador el derecho, pero no la obligación, de comprar o vender un activo subyacente a un precio acordado en una fecha determinada o antes de ella (en caso de ser americana). El activo subyacente puede ser cualquier instrumento que tenga valor de mercado, como una acción, un índice bursátil, una materia prima o una divisa.

Existen dos tipos principales de opciones financieras: las opciones de compra (Call options) y las opciones de venta (Put option). Una opción de compra otorga al comprador el derecho a comprar el activo subyacente a un precio específico, mientras que una opción de venta otorga al comprador el derecho a vender el activo subyacente a un precio específico.

El precio al que se compra la opción se lo denomina prima. Dado que hay un comprador también hay vendedor, también llamado lanzador, quien es el que cobra la prima de estas opciones de compra y/o venta y tienen la obligatoriedad de asumir sus compromisos si el comprador de las opciones ejerce su derecho.

Cuando un inversor compra una opción Call espera que el valor del subyacente suba en los mercados, es decir, tiene expectativas alcistas. Si llegada la fecha de vencimiento (suponiendo que es una opción europea por lo cual solo puede ejercérsela a su vencimiento ), su apuesta resulta acertada y el precio del subyacente es superior al precio de ejercicio fijado en el contrato, le interesará ejercer la opción, ya que puede comprar el activo subyacente más barato para luego venderlo en el mercado y obtener como ganancia la diferencia entre las mismas. Por el contrario, si el precio no sube como esperaba y el precio de ejercicio es mayor que el del subyacente, no ejercerá la opción y perderá la inversión realizada, es decir, la prima.

Por caso contrario y manteniendo la misma lógica en la dinámica, si el comprador ejerce el Put (opción de venta) el lanzador tiene la obligación de comprar el subyacente.

Relación entre precio de mercado y strike

Si relacionamos el precio de mercado y de strike podemos clasificarlas en tres grupos diferentes:

-Opciones ITM (In the money): Son las opciones que se encuentran ejercibles en ese momento. Para el caso de un Call es cuando el strike es menor al precio del subyacente y para el caso del Put cuando el Strike es mayor al precio del subyacente.

-Opciones ATM (At the money): Son las opciones que tienen un Strike igual al precio de mercado en ese momento. Es equivalente para el caso de Calls y Puts.

-Opciones OTM (Out the money): Son las opciones que no se encuentran ejercibles en ese momento. Para el caso de un Call cuando el Strike es mayor al Precio de mercado y para el caso de un Put cuando el Strike es menor al precio de mercado. No tienen valor intrínseco, solo tienen valor tiempo.

También podemos diferenciar las opciones, dependiendo del momento en que pueden ser ejercidas.

Una opción americana es aquella en la que quien posee la opción puede ejercer su derecho de compra o venta del activo subyacente en cualquier momento antes o en la fecha de vencimiento de la opción. Es decir, el comprador de la opción americana puede ejercerla en cualquier momento durante la vida de la opción. Por otro lado, una opción europea es aquella en la que quien posee la opción sólo puede ejercer su derecho de compra o venta del activo subyacente en la fecha de vencimiento de la opción. En otras palabras, el comprador de la opción europea no puede ejercer su derecho antes de la fecha de vencimiento.

Análisis estratégico del ejercicio anticipado en opciones americanas

Como parte de una estrategia de inversión, es crucial analizar la decisión de ejercer una opción americana antes de su vencimiento. Esta característica particular las distingue de las opciones europeas y es importante conocerla para maximizar la rentabilidad.

En el caso de las opciones Call, el ejercicio anticipado tiene un costo importante: se sacrifica el interés que podría generar el capital inmovilizado en el strike. Además, al ejercer de forma prematura, se renuncia al valor tiempo o valor extrínseco que aún le queda a la prima. Este valor extrínseco es la porción de la prima que excede el valor intrínseco de la opción y se ve influenciado por variables como la volatilidad, la tasa de interés y el tiempo restante hasta el vencimiento. A diferencia del valor intrínseco, que es la diferencia entre el strike y el precio de mercado, el valor extrínseco refleja las expectativas futuras del mercado e influye mucho en la valoracion. Este valor adicional podría capturarse vendiendo la opción en el mercado, una estrategia que a menudo resulta más rentable.

No obstante, el principal beneficio del ejercicio anticipado es la posibilidad de capturar un dividendo que de otro modo no se recibiría. Por ello, se considera que el momento óptimo para ejercer una Call es cuando se anuncia un dividendo significativo justo antes de la expiración de la opción.

En contraste, el “Early Exercise” de una opción Put implica un trade-off diferente. El principal beneficio es la ganancia de la tasa de interés sobre el monto del strike, mientras que el costo es la pérdida de cualquier dividendo futuro. El momento ideal para realizarlo es cuando la opción está “deep in the money” y el valor de los dividendos futuros es insignificante en comparación con la ganancia inmediata por intereses.

Podemos clasificar 4 tipos de posiciones básicas:

• Compra de Call (Long call). Denota unaposición alcista ya que si asume esta posición es porque espera que el precio del subyacente se incremente para él y así poder ejecutar dicha opción y tomar ganancia. Es decir, si el precio del activo subyacente sube por encima del precio de ejercicio, el comprador de la opción de compra puede ejercer su derecho de compra y obtener una ganancia. Si el precio del activo subyacente no alcanza el precio de ejercicio, el comprador de la opción de compra perderá el precio de la opción.

• Venta de Call (Short Call). Refleja una Posición bajista dado que el lanzador de dicha opción espera que el activo baje y por lo tanto el tenedor de dicha opción no ejecute su derecho. Por otra parte, el vendedor recibe una prima por vender la opción. Si ocurre el caso contrario de la que espera el vendedor, es decir, el precio del activo subyacente sube por encima del precio de ejercicio, el vendedor de la opción de compra puede enfrentar pérdidas ilimitadas.

• Compra de Put (Long Put). Expresa una posición bajista ya que adquiere el derecho a ejecutar la opción debido a que el precio del subyacente disminuyo y el ganar la diferencia entre el strike y precio de mercado. Por el contrario, si el precio del activo subyacente no cae por debajo del precio de ejercicio, el comprador de la opción de venta perderá el precio de la misma.

• Venta de Put (Short Put). Por último, esta cuarta significa una posición alcista ya que el vendedor espera que no le ejecuten dicho derecho dado que el precio en el mercado va a aumentar y por ende será mayor al del strike. En caso de que el precio del activo subyacente esté por debajo del precio de ejercicio, el vendedor de la opción de venta puede enfrentar pérdidas ilimitadas.

Modelo Black-Scholes

Black-Scholes es un de los modelos matemáticos más utilizados para calcular el precio teórico de opciones financieras. Fue desarrollado por Fischer Black y Myron Scholes en 1973, y luego fue mejorado por Robert Merton.

Antes de surgir este modelo, los inversores y traders utilizaban modelos más simples para valorar opciones, como el modelo de Cox-Ross-Rubinstein. Estos modelos asumían que el precio de la opción se movía en pasos discretos, lo que no reflejaba la realidad del mercado.

El modelo Black-Scholes utiliza varios factores para determinar el precio teórico de una opción, incluyendo el precio del activo subyacente, el precio de ejercicio de la opción, la tasa libre de riesgo, la volatilidad del precio del activo subyacente y el tiempo restante hasta la expiración de la opción.

Este modelo en estudio considera una acción que no paga dividendos y asume que el rendimiento sobre la acción en un periodo corto se distribuye normalmente. También asume que los rendimientos de dos periodos diferentes no superpuestos son independientes.

Las fórmulas de Black-Scholes para calcular los precios de opciones de compra y de venta europeas sobre acciones que no pagan dividendos son:

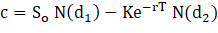
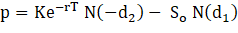
Donde

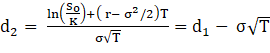
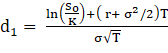
La función N(x) es la función de probabilidad acumulativa para una variable normal estandarizada. En otras palabras, es la probabilidad de que una variable con una distribución normal estándar, (0, 1), sea menor que x.

Cuando el precio de la acción aumenta demasiado, el precio de una opción de venta europea, p, se aproxima a cero. Este resultado concuerda con la ecuación porque N(-d1) y N(-d2) se aproximan a cero cuando S0 es grande.

Cuando el precio de la acción disminuye demasiado, tanto d1 como d2 aumentan mucho y se vuelven negativos. Eso significa que N(d1) y N(d2) están muy próximos a cero y que la ecuación proporciona un precio cercano a cero para la opción de compra.

Las variables c y p son los precios de las opciones de compra y de venta europeas, S0 es el precio de la acción, K es el precio de ejercicio, r es la tasa de interés libre de riesgo (expresada con una composición continua), T es el tiempo al vencimiento y sigma es la volatilidad del precio de la acción.

El único parámetro en las fórmulas de valuación de Black-Scholes que no puede observarse directamente es la volatilidad del precio de la acción. Además de la volatilidad implícita, las letras griegas son fundamentales y muy utilizadas para entender los riesgos.

¿Para qué sirven las famosas letras griegas?

Las letras griegas son términos utilizados en la valoración de opciones, que representan la sensibilidad de los precios de las opciones respecto a determinadas variables. Estas letras se utilizan para medir la volatilidad implícita de las opciones y la exposición a cambios en el precio subyacente, el tiempo y la tasa de interés.

Cada letra griega mide un aspecto diferente del riesgo en una posición en opciones y el objetivo de un negociante es manejar las letras griegas de tal manera que todos los riesgos sean aceptables.

Comenzamos definiendo a Delta que representa la tasa de cambio del precio de la opción con respecto al precio del activo subyacente.

La gamma de una cartera de opciones sobre un activo subyacente es la tasa de cambio de la delta de la cartera con respecto al precio del activo subyacente. Si gamma es pequeña, delta cambia lentamente y los ajustes para mantener una cartera delta neutral deben realizarse sólo en pocas ocasiones. Es decir, esta letra griega está representada por la derivada segunda y es la misma para el Call y el Put de la misma base.

Este es uno de los principales indicadores porque nos indica la aceleración a la que se va a mover la posición comprada o vendida. En simples palabras, Delta es velocidad y Gamma como se acelera dicha posición.

La letra griega Theta representa el cambio en el valor de la prima ante el paso del tiempo. La pérdida del valor tiempo del precio de la prima. La theta es usualmente negativa para una opción. Esto se debe a que conforme el tiempo al vencimiento disminuye y todo lo demás permanece constante, el valor de la opción tiende a disminuir.

La Vega por su parte, es el cambio en el precio de la prima ante cambio de la volatilidad. Nunca tiene valores negativos. Si la vega es alta en términos absolutos, el valor de la cartera es muy sensible a pequeños cambios en la volatilidad. Si la vega es baja en términos absolutos, los cambios en la volatilidad tienen un impacto relativamente bajo en el valor de la cartera.

Por último Rho de una cartera de opciones es la tasa de cambio del valor de la cartera con respecto a la tasa de interés.

En la segunda parte de este informe, en el newsletter del mes que viene, profundizaremos en la aplicación práctica de estos conceptos, analizando estrategias como el straddle y cómo el cálculo del “Expected Move” nos permite anticipar y capitalizar la volatilidad del mercado en eventos clave como la temporada de resultados, momento en que todas las empresas reportan sus balances.